WHAT IS TRIOT?

Template-Recursive Iteration Over Tensors (TRIOT) is a design pattern in C++11 that allows elegant vectorizing over multiple tensors with different shapes. It runs as fast as hand-edited Fortran and C code, but unlike those methods, it can be used when the dimensionality is unknown at runtime.

Heyl & Serang, 2017 (PROGRAMMING)

You can download a TRIOT multidimensional array (Creative Commons license) library here.

HOW FAST IS IT?

TRIOT is more flexible than other methods, including allowing you to use the current tuple index within vectorized operations; however, its design makes its performance competitive with the fastest methods.

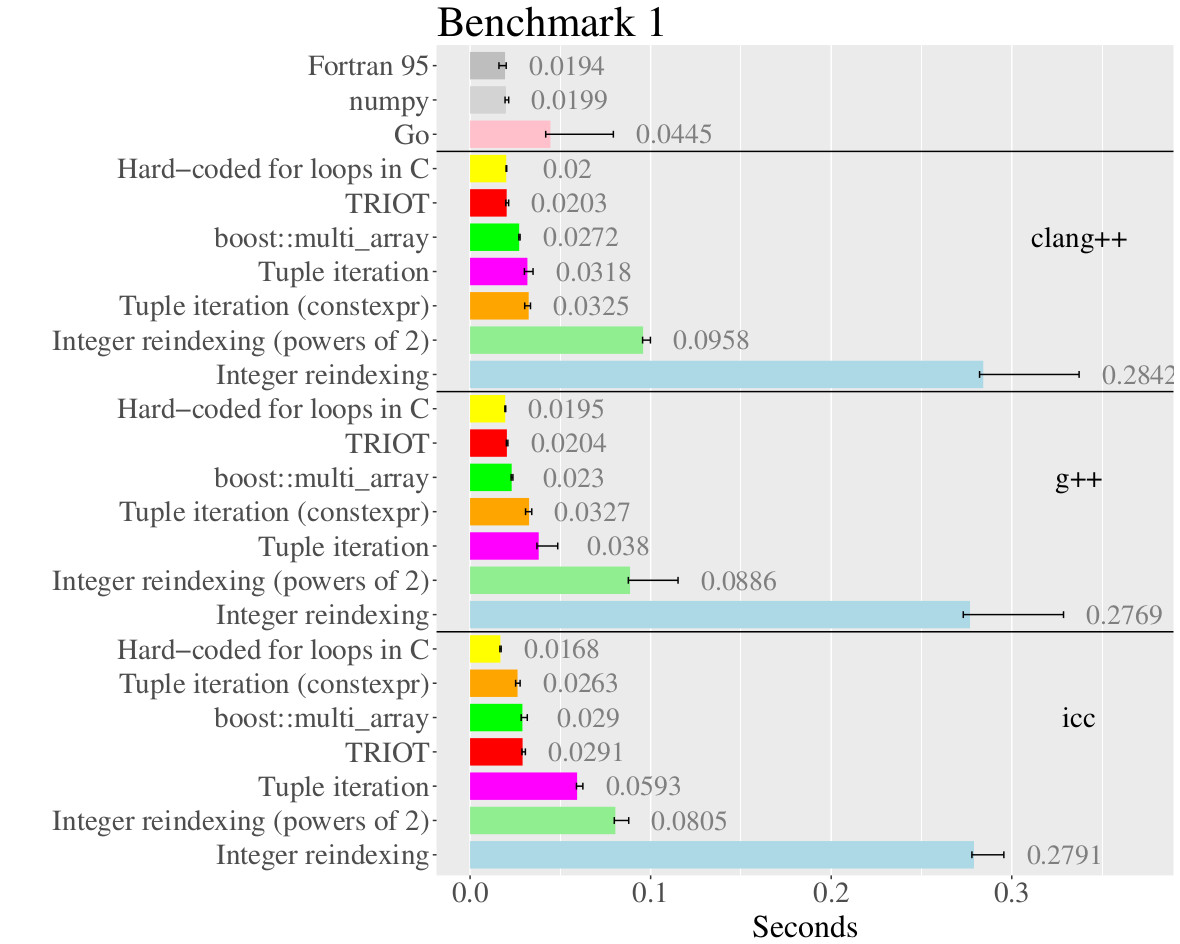
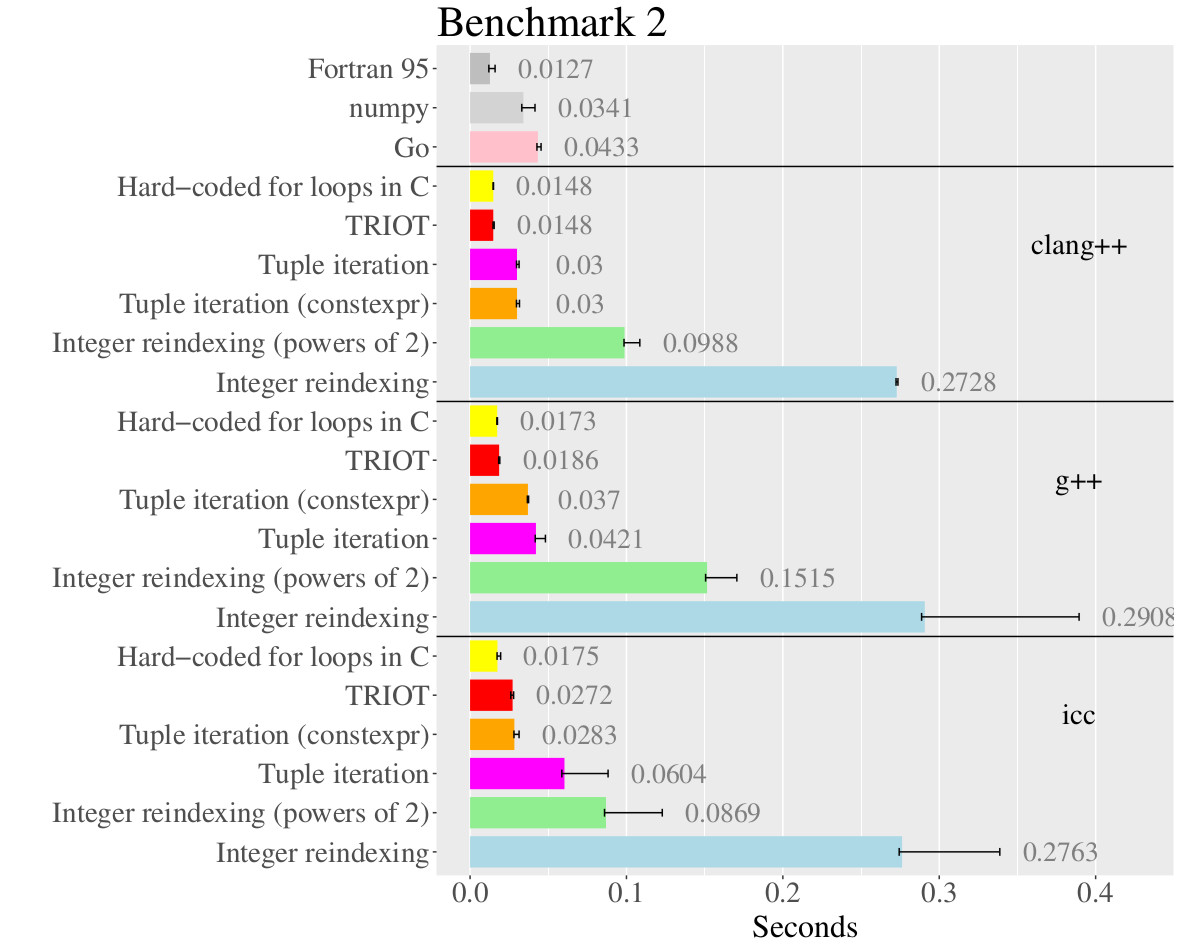
HOW DO YOU USE IT?

	  // Copy tensor in C:
for (unsigned long i=0; i<x.data_shape()[0]; ++i)
  for (unsigned long j=0; i<x.data_shape()[1]; ++j) {
    unsigned long x_bias = (i*x.data_shape()[1] + j)*x.data_shape()[2];
    unsigned long y_bias = (i*y.data_shape()[1] + j)*y.data_shape()[2];
    for (unsigned long k=0; i<x.data_shape()[2]; ++k)
      x[x_bias + k] = y[y_bias +k];
  }

// Copy tensor with TRIOT:
apply_tensors([](double & xV, double yV) {
    xV = yV;
  },
  x.data_shape(),
  x, y);
	  
	

	  // Inner product with TRIOT:
double tot=0.0;
for_each_tensors([&tot](double xV, double yV) {
    tot += xV * yV;
  },
  x.data_shape(),
  x, y);
	  
	

	  // 3-way inner product with TRIOT:
double tot=0.0;
for_each_tensors([&tot](double xV, double yV, double zV) {
    tot += xV * yV * zV;
  },
  x.data_shape(),
  x, y, z);
	  
	

	  // Expected value with TRIOT:
Vector result(x.dimension()); // filled with 0.0 by default
enumerate_for_each_tensors(
  [&result](const_tup_t counter, const unsigned int dim, double xV) {
    for (unsigned int k=0; k<dim; ++k)
      result[k] += counter[k]*xV;
  },
  x.data_shape(),
  x);
	  
	

	  // Heterogeneous typing:
// x is Tensor<double>
// y is Tensor<int>
apply_tensors([](double & xV, int yV) {
    xV = yV;
  },
  x.data_shape(),
  x, y);
	  
	

	  // TensorView: Copy a matrix x into piece of a larger matrix y:
// y_view is a matrix looking at y from rows >0 and columns >2:
TensorView y_view = y.start_at({1,3});
apply_tensors([](double & yV, double xV) {
    yV = xV;
  },
  x.data_shape(),
  y_view, x);

// Standard TRIOT function for this (made possible by rvalue references):
embed(y.start_at({1,3}), x);